Personalized Decision Modeling: Utility Optimization or Textualized‑Symbolic Reasoning

Yibo Zhao ¹

Yang Zhao ¹

Hongru Du ² ^*,†

Hao (Frank) Yang ¹ ^†

¹ Johns Hopkins University

² University of Virginia

NeurIPS 2025 (Spotlight)

^* This work was completed while Hongru Du was at Johns Hopkins University.

^† Correspondence to: Hongru Du and Hao (Frank) Yang.

Paper (PDF) Code (coming soon) Arxiv

Abstract

We study personalized decision modeling in settings where individual choices deviate from population-optimal predictions. We introduce ATHENA—an Adaptive Textual‑symbolic Human‑centric Reasoning framework—built in two stages: (1) a group‑level symbolic utility discovery procedure (LLM‑augmented symbolic search) learns compact, interpretable utility forms; and (2) an individual‑level semantic adaptation step refines a personal template with TextGrad to capture each person’s preferences and constraints. On Swissmetro (travel mode choice) and COVID‑19 vaccine uptake tasks, ATHENA consistently outperforms utility‑based, ML, and LLM baselines, improving F1 by ≥ 6.5% over the strongest alternatives while maintaining calibrated probabilistic predictions. Together, these stages bridge classic Random Utility Maximization with textual semantic context, yielding interpretable structure and personalized reasoning.

Method at a Glance

{f^t_{g,k}}_{k=1}^K \sim \phi(\cdot \mid g, C, S, B^{t-1})

Group-level Symbolic Utility Discovery samples candidate symbolic utility functions ${f^t_{g,k}}_{k=1}^K$ from the LLM-conditioned distribution $\phi(\cdot \mid g, C, S, B^{t-1})$ , guided by the concept library $C$ , symbolic library $S$ , and prior feedback $B^{t-1}$ .

P^{t+1}_i \leftarrow P^t_i - \eta\,\nabla_{P_i} \, \mathcal{L}(P^t_i, D_i)

Individual-level Semantic Adaptation refines each person’s $P_i$ through iterative updates. This process personalizes the template based on individual data $D_i$ and semantic gradients, capturing heterogeneous preferences and contextual constraints.

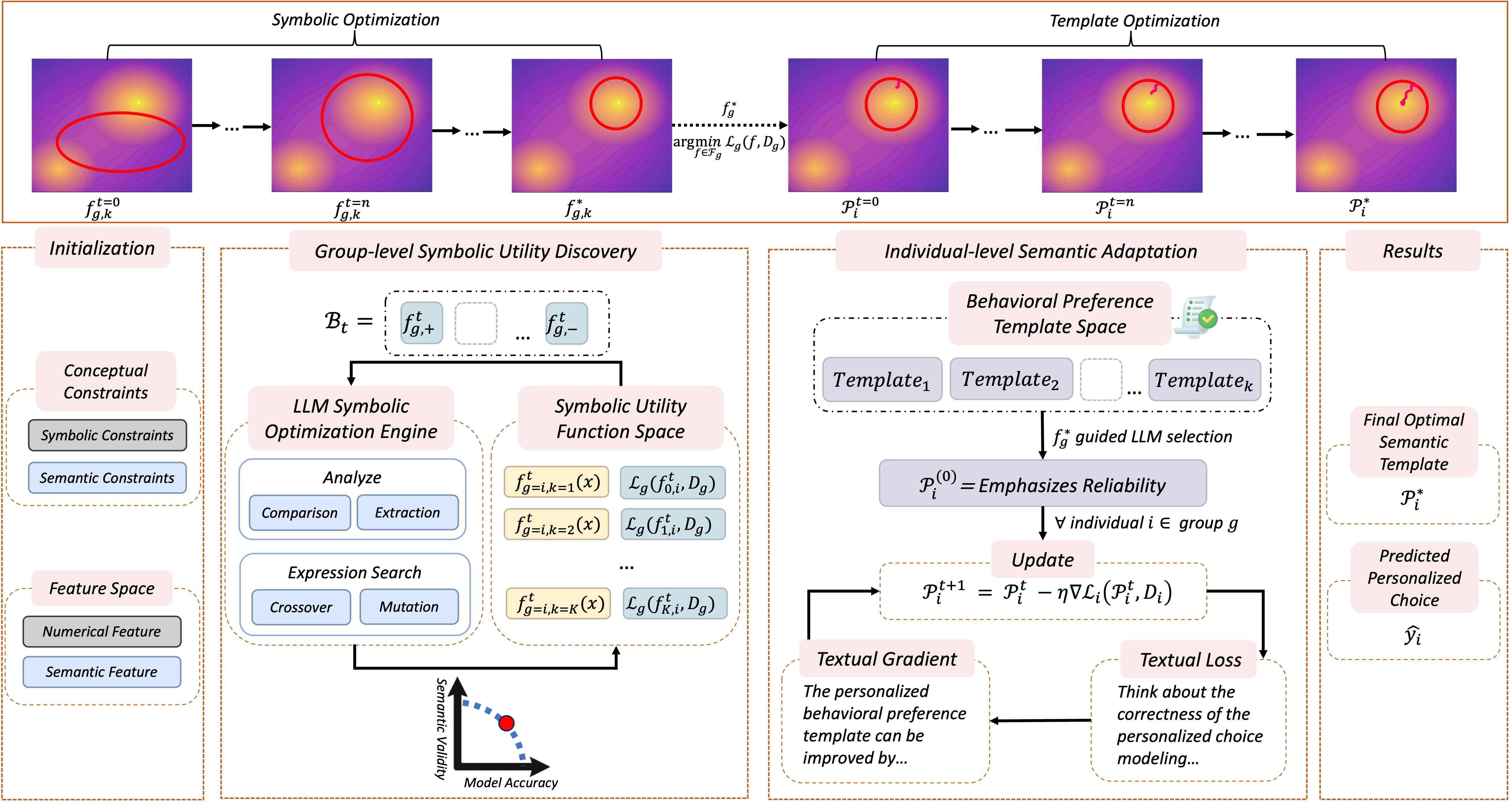
Two-stage ATHENA pipeline combining symbolic discovery and semantic adaptation — **Figure 1:** Overview of **ATHENA** framework. The *Group-level symbolic utility discovery* stage uses an LLM-driven symbolic optimization to find compact utilities  $f_g^*$ . The *Individual-level semantic adaptation* stage refines personalized templates  $\mathcal{P}_i^*$  via TextGrad to model individual decision rules.

Two‑Stage Pipeline

Group‑Level Symbolic Utility Discovery LLMs sample candidate symbolic utility functions (Eq. 3) from a structured symbolic–semantic space, guided by a concept library  $C$  and feedback  $B^{t-1}$ . Through iterative evaluation and mutation/crossover, the model converges to the optimal symbolic utility  $f_g^*$  that best captures group‑level decision regularities.
Individual‑Level Semantic Adaptation Using the discovered  $f_g^*$  as a strong prior, each individual’s textual semantic template  $P_i$  is optimized by TextGrad (Eq. 7) to incorporate heterogeneous personal preferences and constraints. The adaptation continues until the template converges to  $P_i^*$ .

\hat{y}_i \sim \phi\big(P_i^*, X_i \,\big|\, f_g^*(X_i; \theta_g^*)\big)

Personalized Decision Inference integrates the learned symbolic utility  $f_g^*$  with the adapted semantic template  $P_i^*$  to generate individualized predictions  $\hat{y}_i$  that reflect both group‑level reasoning and personal context.

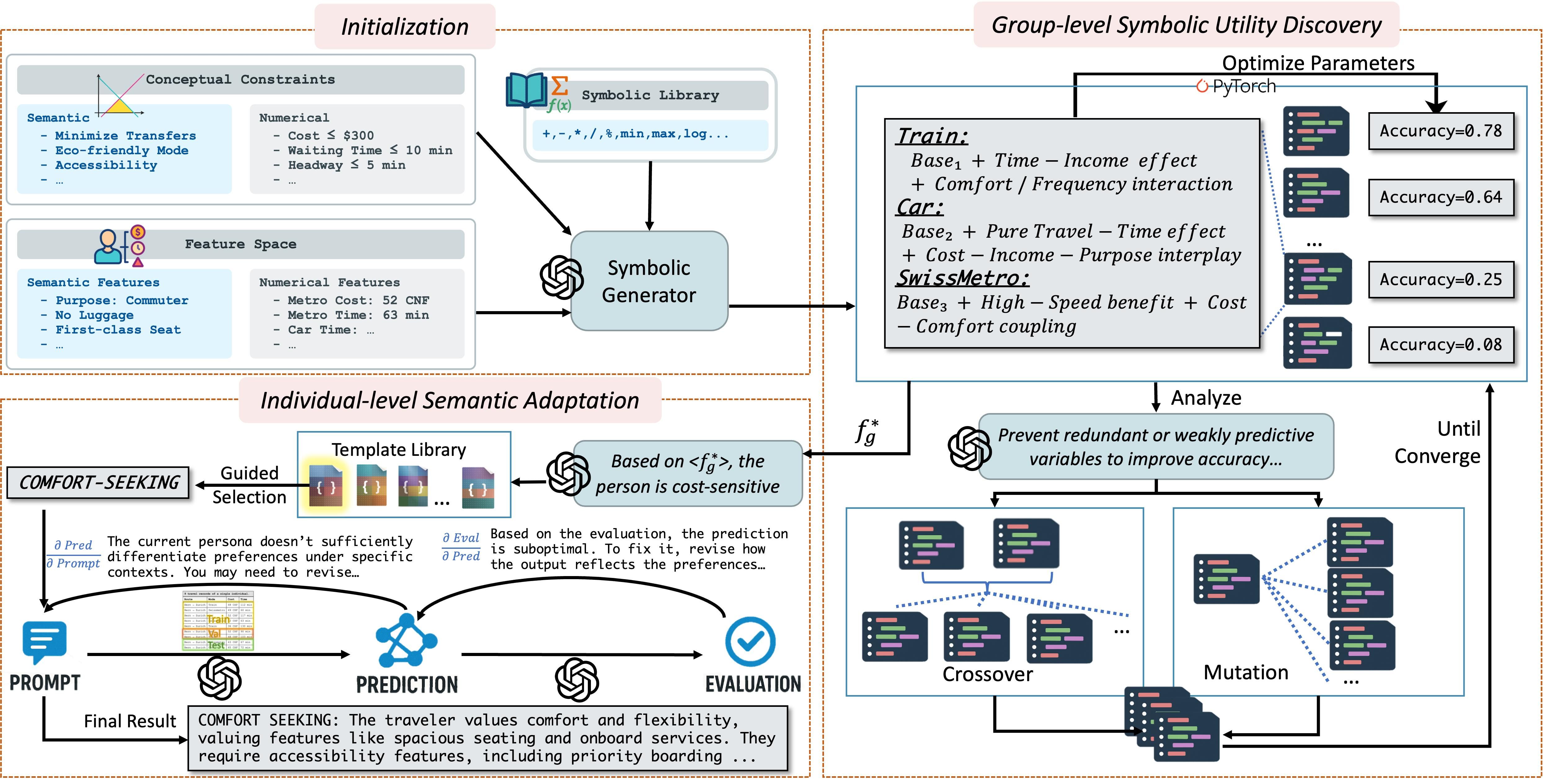
Optimization flow diagram showing symbolic feedback and TextGrad updates — **Figure 2:** **ATHENA pipeline applied to travel–mode choice.** Using *Swissmetro* as an example, the *Initialization* encodes constraints and symbolic features. In *Group-level optimization*, LLMs sample and prune utility formulas  $\{f_g^*\}$ . In *Individual adaptation*, each  $f_g^*$  guides a personalized prompt  $\mathcal{P}_i^*$  to capture heterogeneity.

Algorithm 1 · ATHENA Optimization Flow

Require Demographic group $g$ , dataset $\mathcal{D}_g$ , domain concept $\mathcal{C}$ , symbolic building block $\mathcal{S}$
Initialize $\mathcal{B}_0 \leftarrow \texttt{None}$
// Stage 1: Group-Level Symbolic Utility Discovery
for $t = 1 \text{ to } T$ do
Sample symbolic utility functions $\{f_{g,k}^{t}\}_{k=1}^K \sim \phi(\cdot \mid g, \mathcal{C}, \mathcal{S}, \mathcal{B}^{t-1})$
Update $\mathcal{B}^t \leftarrow \{f_{g,+}^t, f_{g,-}^t\}$ using Eq. $(3)$
Select best function $f_g^* \leftarrow \arg\min_{f \in \mathcal{F}_g} \mathcal{L}_g(f, \mathcal{D}_g)$
ifstopping condition in Eq. $(4)$ then break
// Stage 2: Individual-Level Semantic Adaptation
for eachindividual $i \in g$
Initialize semantic template $\mathcal{P}_i^{0} \sim \phi( \cdot \mid f_g^*, i, \mathcal{C})$
for $t = 1 \text{ to } T'$ do
Update $\mathcal{P}_i^{t+1} \leftarrow \mathcal{P}_i^{t} - \eta \nabla \mathcal{L}_i(\mathcal{P}_i^{t}, \mathcal{D}_i)$ using Eq. $(7)$
return $\{\mathcal{P}_i^{*}\}_{i \in g}$ , predict decisions using Eq. $(8)$

Results

Overall Performance

Performance comparison of LLM-based, classical choice, and machine learning methods on the three-class Swissmetro and three-class COVID-19 Vaccine choice tasks.
	Method	LLM Model	Swissmetro				Vaccine
			Acc. ↑	F1. ↑	CE ↓	AUC ↑	Acc. ↑	F1. ↑	CE ↓	AUC ↑
LLM- Based	Zeroshot	gemini-2.0-flash	0.5920	0.2940	0.9257	0.6561	0.5800	0.5092	0.8328	0.7607
	Zeroshot	GPT-4o-mini	0.6300	0.2757	2.7258	0.3657	0.5433	0.5387	0.8562	0.7395
	Zeroshot-CoT	gemini-2.0-flash	0.5880	0.3478	0.9415	0.6331	0.5800	0.5073	0.8436	0.7526
	Zeroshot-CoT	GPT-4o-mini	0.6420	0.2960	0.8957	0.6237	0.5500	0.5353	0.8540	0.7465
	Fewshot	gemini-2.0-flash	0.7580	0.7027	8.7244	0.7956	0.5667	0.5740	12.0324	0.7053
	Fewshot	GPT-4o-mini	0.6815	0.4945	7.0029	0.7395	0.5067	0.5097	6.6110	0.6891
	TextGrad	gemini-2.0-flash	0.5568	0.2980	1.2011	0.5400	0.4241	0.4014	5.7813	0.6363
	TextGrad	GPT-4o-mini	0.6500	0.3620	0.9079	0.5364	0.5084	0.4962	4.5412	0.6709
	ATHENA	gemini-2.0-flash	0.7679	0.7222	0.9041	0.8387	0.6797	0.5968	0.7610	0.8370
	ATHENA	GPT-4o-mini	0.8134	0.7655	1.0863	0.8825	0.7345	0.7161	0.7551	0.8704
Utility Theory	MNL	/	0.6101	0.3887	0.8353	0.7074	0.4150	0.1955	1.0510	0.4301
	CLogit	/	0.5714	0.2424	0.8916	0.5976	0.4150	0.1955	1.0510	0.5000
	Latent Class MNL	/	0.6101	0.3967	0.8175	0.7182	0.1950	0.1088	1.0986	0.5000
Machine Learning	Logistic Regression	/	0.5620	0.5570	0.9310	0.7460	0.6500	0.6690	0.7630	0.8330
	Random Forest	/	0.7100	0.7050	0.7380	0.8810	0.6300	0.6470	0.7290	0.8420
	XGBoost	/	0.7080	0.7050	0.7040	0.8810	0.6300	0.6480	1.1420	0.8150
	BERT	/	0.7246	0.4994	0.7037	0.8811	0.6350	0.6541	0.7409	0.8168
	TabNet	/	0.6375	0.4060	0.7887	0.8810	0.6650	0.6684	0.8968	0.8147
	MLP	/	0.6475	0.6386	0.7626	0.8350	0.6068	0.6062	0.9320	0.8205

BibTeX

@inproceedings{zhao2025athena,
  title        = {Personalized Decision Modeling: Utility Optimization or Textualized-Symbolic Reasoning},
  author       = {Yibo Zhao, Yang Zhao, Hongru Du, Hao Frank Yang},
  booktitle    = {The Thirty-Ninth Annual Conference on Neural Information Processing Systems (NeurIPS)},
  year         = {2025}
}